
Home Research CV Coding Photography
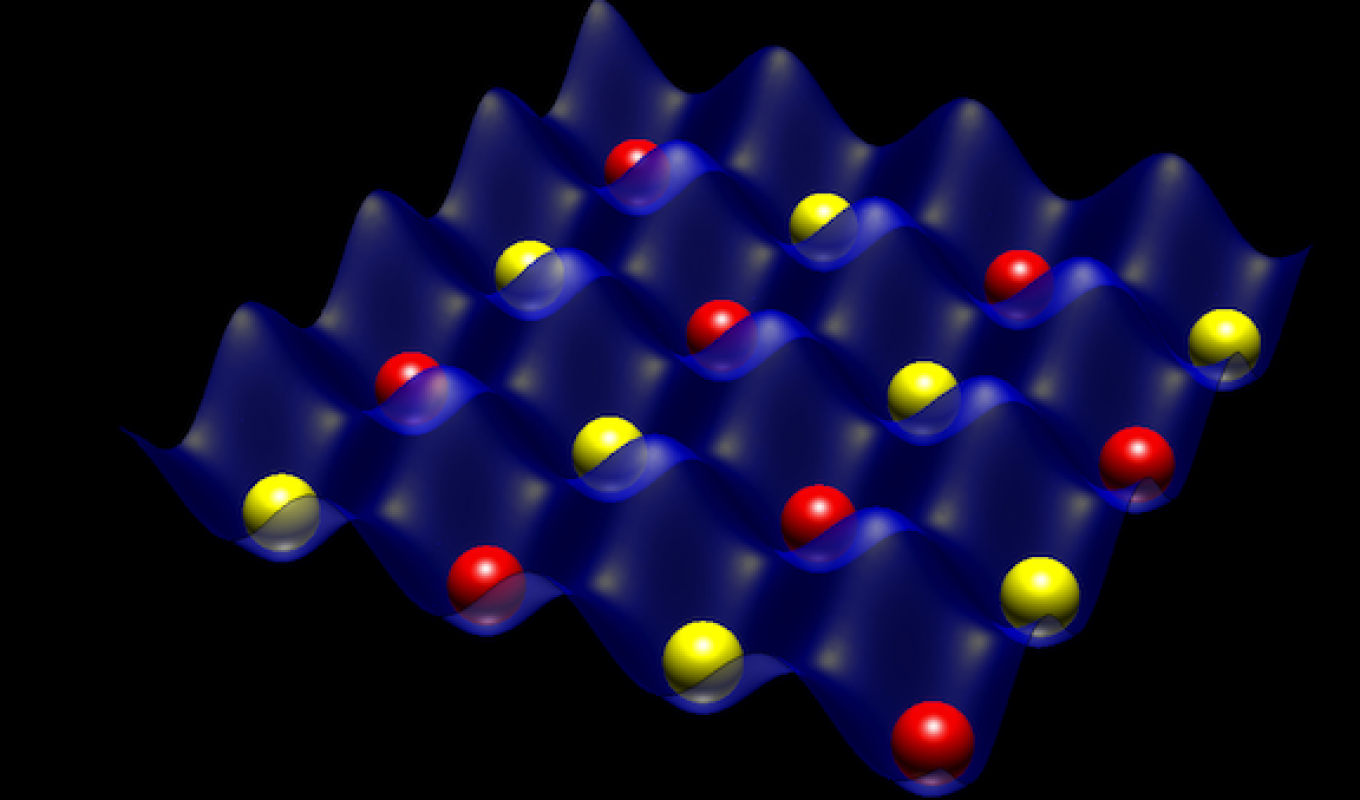 The figure to the left shows the schematic of an optical lattice with trapped atoms. Before delving deeper into the physics of it, let us first understand what an "optical lattice" is. To begin with, let us start with the all familiar term, "crystal". A perfect crystal is an array of atoms or group of atoms, where a given arrangement is repeated forming a periodic structure. Imagine if we were to replace the group of atoms by "points" in a 3D space, we will be left with just the structure with periodically repeated points. This abstract periodic structure is called the "lattice" and the points can be referred to as "lattice" sites. The branch of physics dealing with such systems (and a lot more!) is often referred to as condensed matter physics. The figure to the left shows such a crystal structure, where the red and yellow atoms are periodically repeated in an underlying "lattice". This schematic, however, does not show a naturally occuring crystal, but one that hss been engineered using lasers. Hence, the term "optical lattice". A periodic lattice can be formed simply by overlapping two counter-propagating laser beams. The interference between the two laser beams form an optical standing wave. By interfering more laser beams, one can obtain one-, two- and three-dimensional (1D, 2D and 3D) periodic lattices.
"Ultra-cold"
atoms can be trapped in such optical lattices, to create crystal structures reminiscent of ordinary crystals. However, unlike traditional condensed matter systems, the lattice properties (such as the trapping depth and the lattice structure) can be changed in real time during an experiment. This control allows one to perform range of experiments with applications to quantum computing and quantum emulation of condensed matter systems. A very good review can be found here.
The figure to the left shows the schematic of an optical lattice with trapped atoms. Before delving deeper into the physics of it, let us first understand what an "optical lattice" is. To begin with, let us start with the all familiar term, "crystal". A perfect crystal is an array of atoms or group of atoms, where a given arrangement is repeated forming a periodic structure. Imagine if we were to replace the group of atoms by "points" in a 3D space, we will be left with just the structure with periodically repeated points. This abstract periodic structure is called the "lattice" and the points can be referred to as "lattice" sites. The branch of physics dealing with such systems (and a lot more!) is often referred to as condensed matter physics. The figure to the left shows such a crystal structure, where the red and yellow atoms are periodically repeated in an underlying "lattice". This schematic, however, does not show a naturally occuring crystal, but one that hss been engineered using lasers. Hence, the term "optical lattice". A periodic lattice can be formed simply by overlapping two counter-propagating laser beams. The interference between the two laser beams form an optical standing wave. By interfering more laser beams, one can obtain one-, two- and three-dimensional (1D, 2D and 3D) periodic lattices.
"Ultra-cold"
atoms can be trapped in such optical lattices, to create crystal structures reminiscent of ordinary crystals. However, unlike traditional condensed matter systems, the lattice properties (such as the trapping depth and the lattice structure) can be changed in real time during an experiment. This control allows one to perform range of experiments with applications to quantum computing and quantum emulation of condensed matter systems. A very good review can be found here.
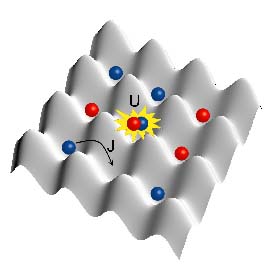 Atoms trapped in the optical lattice are necessarily not immobile, and can actually hop from one lattice site to another, a process called quantum mechanical
tunneling.
Its essentially a quantum phenomena where a particle "leaks" out "through" a barrier which is otherwise energetically insurmountable. Such behavior becomes extremely important in the microscopic realm, where particles behave nothing like "billiard balls". In fact, they behave more like waves characterized by a wave function, with only a probability of finding the particle at a given point in space. This hopping is characterized by the tunneling energy J. In addition to J, the atoms also interact repulsively with interaction energy U whenever two or more such atoms occupy the same site. Thus, hopping to an already occupied site costs energy. In essence, it is a dynamic system, and is well described by the
Bose–Hubbard model.
The interplay between U and J determines the physics of the system. For weak interactions relative to the tunneling energy, U/J << 1, the system forms a
Bose–Einstein condensed state
of matter, where each atom is delocalized over the entire lattice. Such a state is favoured as the hopping term is minimized for single-particle wavefunctions spread out throughout the lattice. In this case, the total system can be described by a giant matter wave and the atom number per lattice site follows a poissonian distribution. For the case of large interactions relative to the kinetic energy, U/J >> 1, the system enters the strongly correlated state of a Mott insulator, in which the atoms are localized to single lattice sites, with a fixed particle number per site. An excellent review on the recent experimental and theoretical advances in this field can be found
here.
Atoms trapped in the optical lattice are necessarily not immobile, and can actually hop from one lattice site to another, a process called quantum mechanical
tunneling.
Its essentially a quantum phenomena where a particle "leaks" out "through" a barrier which is otherwise energetically insurmountable. Such behavior becomes extremely important in the microscopic realm, where particles behave nothing like "billiard balls". In fact, they behave more like waves characterized by a wave function, with only a probability of finding the particle at a given point in space. This hopping is characterized by the tunneling energy J. In addition to J, the atoms also interact repulsively with interaction energy U whenever two or more such atoms occupy the same site. Thus, hopping to an already occupied site costs energy. In essence, it is a dynamic system, and is well described by the
Bose–Hubbard model.
The interplay between U and J determines the physics of the system. For weak interactions relative to the tunneling energy, U/J << 1, the system forms a
Bose–Einstein condensed state
of matter, where each atom is delocalized over the entire lattice. Such a state is favoured as the hopping term is minimized for single-particle wavefunctions spread out throughout the lattice. In this case, the total system can be described by a giant matter wave and the atom number per lattice site follows a poissonian distribution. For the case of large interactions relative to the kinetic energy, U/J >> 1, the system enters the strongly correlated state of a Mott insulator, in which the atoms are localized to single lattice sites, with a fixed particle number per site. An excellent review on the recent experimental and theoretical advances in this field can be found
here.
My research involves theoretically studying such systems of trapped atoms in optical lattices. We have been studying extended Bose-Hubbard models that include the effect of higher energy bands, and hopping beyond neighboring lattice sites. In particular, we studied the formation of Bose-Einstein condensates in the higher band of an optical lattice, and the subsequent decay processes. We recently showed that the low energy states of a system of trapped atoms in a double-well optical lattice can emulate a Hubbard model with strong effective three-body interactions. We have devised unique ways to numerically obtain localized Wannier functions that are "real-valued", and have been studying systems of trapped atoms in asymmetric lattices.
Apart from analytical methods, much of the work that I do involves extensive numerical computations. I used to primarily use Fortran 90 coupled with gnuplot for plotting. During the last couple of years, however, I have started using Python more often. I am quite proficient with Mathematica and also familiar with C++. All of my research work is done in a linux system, mainly Ubuntu in my laptop, or Red Hat Enterprise Linux in my office desktop.